|
Главная\Документы\Для учителя математики, алгебры, геометрии При использовании материалов этого сайта - АКТИВНАЯ ССЫЛКА и размещение баннера -ОБЯЗАТЕЛЬНО!!!
Разработка урока по алгебре в 9 классе.Розробка уроку по алгебрі у 9 классі.
Материалы прислала: Федорок Татьяна
Остаповна
учитель-методист,
учитель математики СШ № 4
г. Борислав, Львовская область
tetost2007@ukr.net
Алгебра, 9 клас Тема: Найпростіші перетворення графіків функцій.
Практичне заняття
з використанням комп’ютерної програми Chart2002, складеної Н. Яремчуком.
Мета уроку:
Будуючи графіки з використанням
комп’ютерної програми, вивести основні правила побудови графіків функції у = f(x+a), y = f(x)+a, y = – f(x),
y = f(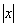 ), y = ), y = 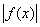 графіка функції y=f(x). графіка функції y=f(x).
Основна частина уроку.
Відкривши вікно
програми, учні ознайомлюються з її основними функціями, можливостями зміни
кольору графіка, кроку та одиничного відрізка.
Після цього
вчитель наводить правила запису формул
функцій у програмі
( англійською
мовою, з використанням символів *, ^, / , abs для позначення модуля, sqrt для позначення квадратного
кореня та інших).
В одній системі
координат різними кольорами учні будують графіки функцій у = х2, у = х2+2, у = х2–2,
у
= х2–3, у = х2+1
та роблять висновок, що графік функції y= f(x) + a може бути одержаний із графіка
функції y= f(x) шляхом паралельного перенесення
його вздовж осі ОУ на  одиниць вгору, якщо а > 0 і
вниз, якщо а < 0 . Висновок учні записують в зошиті. одиниць вгору, якщо а > 0 і
вниз, якщо а < 0 . Висновок учні записують в зошиті.
Далі, очистивши
вікно програми , учні знову в одній системі координат будують графіки функцій у = х2, у = (х–2)2,
у = (х+2)2, у =(х–3)2, у = (х+1)2, та роблять висновок,
що графік функції y= f(x + a) може бути одержаний із
графіка функції y= f(x) шляхом паралельного перенесення
його вздовж осі ОХ на  одиниць вліво, якщо а > 0 і вправо,
якщо а < 0 . Висновок учні записують в зошиті. одиниць вліво, якщо а > 0 і вправо,
якщо а < 0 . Висновок учні записують в зошиті. На наступному
етапі уроку вчитель пропонує учням побудувати в зошитах, використовуючи шаблон
параболи у = х2, графіки
функцій у = (х+3)2, у = х2–1
та
у = (х+2)2 +1, у = (х–1)2
–2.
Продовженням
практичної роботи є побудова графіка функції у = х2–2х
+ 3 . Виконавши виділення повного
квадрата ( із записами на дошці і в зошитах), учні приводять цю формулу до виду
у = (х-1)2+2 та, за
допомогою шаблона параболи
у = х2, за правилами перетворень будують цей графік у
себе в зошитах. Після чого перевіряють правильність побудови за допомогою
програми Chart2002 та , змінивши колір лінії, в тій самій системі
координат будують графік функції
у = х2 –2 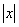 +3 . Разом з учнями вчитель робить
висновок, що для побудови графіка
функції y=f( +3 . Разом з учнями вчитель робить
висновок, що для побудови графіка
функції y=f(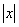 ) слід відкинути частину графіка y= f(x),
яка відповідає від’ємним значенням змінної х
і виконати симетрію відносно осі Оу тієї частини графіка, що відповідає
додатним значенням змінної х. ) слід відкинути частину графіка y= f(x),
яка відповідає від’ємним значенням змінної х
і виконати симетрію відносно осі Оу тієї частини графіка, що відповідає
додатним значенням змінної х.
Аналогічно,
виконуючи на екрані комп’ютера побудови графіків функцій
у =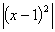 , у = , у = 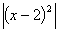 , у = , у =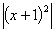 , у = , у = 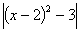 , учні роблять
висновок , що графік функції у = , учні роблять
висновок , що графік функції у = 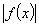 можна отримати із графіка функції
у = f(х) , якщо виконаємо симетрію відносно осі ОХ тієї частини графіка функції
у = f(х) , що міститься під цією віссю. можна отримати із графіка функції
у = f(х) , якщо виконаємо симетрію відносно осі ОХ тієї частини графіка функції
у = f(х) , що міститься під цією віссю.
На
заключному етапі уроку учні опрацьовують в групах способи побудови графіків
функцій у = 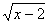 , у = , у = 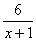 , у = , у =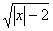 та у = та у = 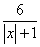 . Представник кожної із груп ( не обов’язково консультант)
розповідає, як побудувати один із
графіків. Учні будують ці графіки на екрані комп’ютера. Для роботи вдома
учням пропонується вивчити сформульовані правила побудови графіків за допомогою
геометричних перетворень і виконати побудови графіків у = . Представник кожної із груп ( не обов’язково консультант)
розповідає, як побудувати один із
графіків. Учні будують ці графіки на екрані комп’ютера. Для роботи вдома
учням пропонується вивчити сформульовані правила побудови графіків за допомогою
геометричних перетворень і виконати побудови графіків у =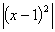 , у = , у = 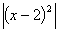 , у = , у = 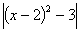 на основі графіка у = х2, та у = на основі графіка у = х2, та у = 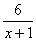 , у = , у = 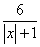 на основі графіка
функції у = на основі графіка
функції у = 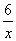 . .
Разработка урока по алгебре в 9 классе.
Розробка уроку по алгебрі у 9 классі.
-
|
